reading-notes
https://faroukibrahim-fii.github.io/reading-notes/
Machine Learning Intro
Chapter 1: Bird’s Eye View
Generally speaking, we can break down applied machine learning into the following chunks:

We will cover exploratory analysis, data cleaning, feature engineering, algorithm selection, and model training.
Chapter 2: Exploratory Analysis
Why explore your dataset upfront?
The purpose of exploratory analysis is to “get to know” the dataset. Doing so upfront will make the rest of the project much smoother, in 3 main ways:
- You’ll gain valuable hints for Data Cleaning (which can make or break your models).
- You’ll think of ideas for Feature Engineering (which can take your models from good to great).
- You’ll get a “feel” for the dataset, which will help you communicate results and deliver greater impact.
Start with Basics
Example observations
| tx_price | beds | baths | sqft | year_built | lot_size | property_type | exterior_walls | roof | basement | restaurants | groceries | nightlife | cafes | shopping | arts_entertainment | beauty_spas | active_life | median_age | married | college_grad | property_tax | insurance | median_school | num_schools | tx_year | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 295850 | 1 | 1 | 584 | 2013 | 0 | Apartment / Condo / Townhouse | Wood Siding | NaN | NaN | 107 | 9 | 30 | 19 | 89 | 6 | 47 | 58 | 33.0 | 65.0 | 84.0 | 234.0 | 81.0 | 9.0 | 3.0 | 2013 |
| 1 | 216500 | 1 | 1 | 612 | 1965 | 0 | Apartment / Condo / Townhouse | Brick | Composition Shingle | 1.0 | 105 | 15 | 6 | 13 | 87 | 2 | 26 | 14 | 39.0 | 73.0 | 69.0 | 169.0 | 51.0 | 3.0 | 3.0 | 2006 |
| 2 | 279900 | 1 | 1 | 615 | 1963 | 0 | Apartment / Condo / Townhouse | Wood Siding | NaN | NaN | 183 | 13 | 31 | 30 | 101 | 10 | 74 | 62 | 28.0 | 15.0 | 86.0 | 216.0 | 74.0 | 8.0 | 3.0 | 2012 |
| 3 | 379900 | 1 | 1 | 618 | 2000 | 33541 | Apartment / Condo / Townhouse | Wood Siding | NaN | NaN | 198 | 9 | 38 | 25 | 127 | 11 | 72 | 83 | 36.0 | 25.0 | 91.0 | 265.0 | 92.0 | 9.0 | 3.0 | 2005 |
| 4 | 340000 | 1 | 1 | 634 | 1992 | 0 | Apartment / Condo / Townhouse | Brick | NaN | NaN | 149 | 7 | 22 | 20 | 83 | 10 | 50 | 73 | 37.0 | 20.0 | 75.0 | 88.0 | 30.0 | 9.0 | 3.0 | 2002 |
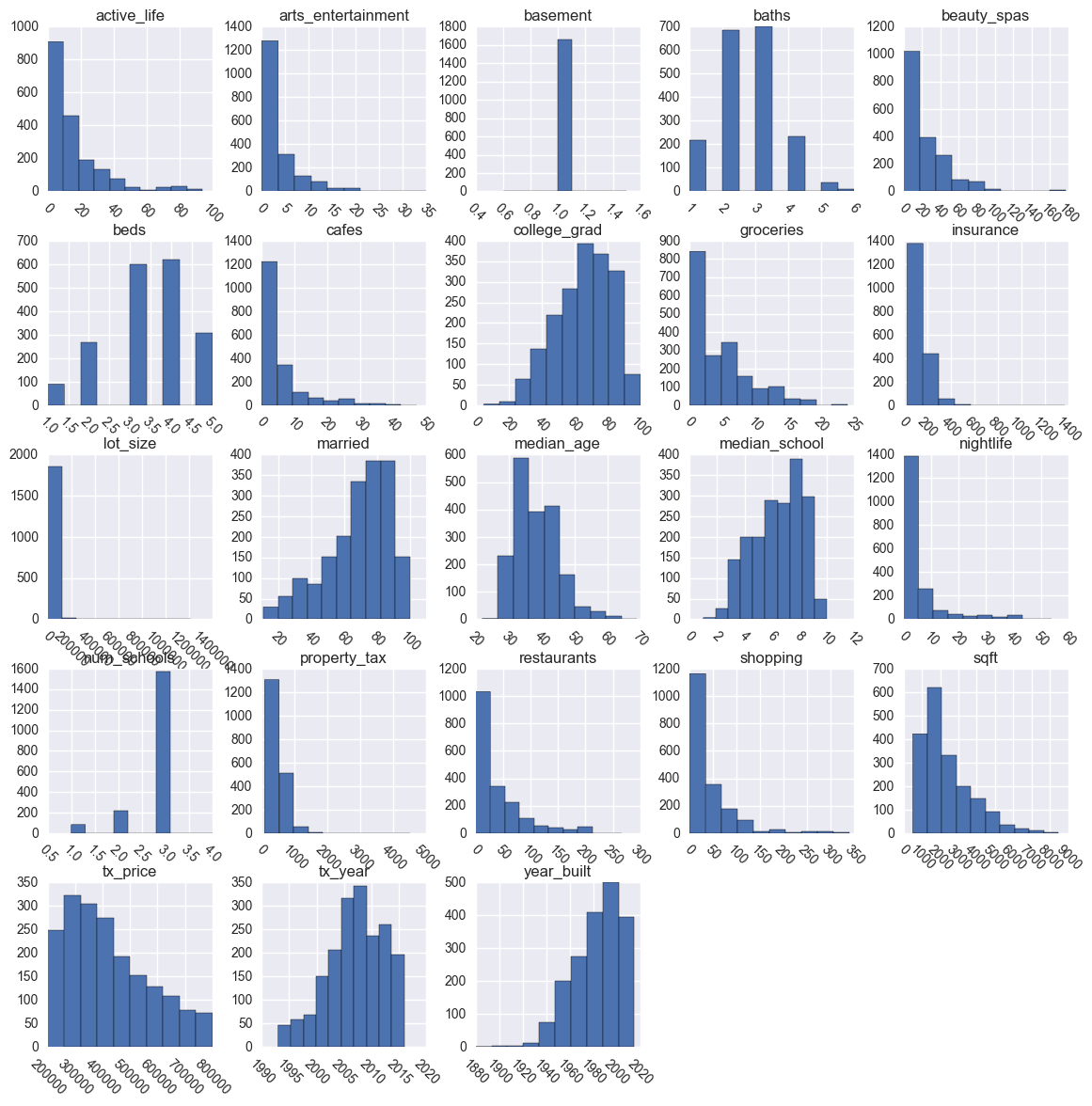
Plot Numerical Distributions
Next, it can be very enlightening to plot the distributions of your numeric features.
Often, a quick and dirty grid of histograms is enough to understand the distributions.
Plot Categorical Distributions
Categorical features cannot be visualized through histograms. Instead, you can use bar plots.
In particular, you’ll want to look out for sparse classes, which are classes that have a very small number of observations.

Plot Segmentations
Segmentations are powerful ways to observe the relationship between categorical features and numeric features.
Box plots allow you to do so.

Study Correlations
Finally, correlations allow you to look at the relationships between numeric features and other numeric features.
Correlation is a value between -1 and 1 that represents how closely two features move in unison.

Chapter 3: Data Cleaning
Better Data > Fancier Algorithms
Data cleaning is one those things that everyone does but no one really talks about. Sure, it’s not the “sexiest” part of machine learning. And no, there aren’t hidden tricks and secrets to uncover.
However, proper data cleaning can make or break your project. Professional data scientists usually spend a very large portion of their time on this step.
Better data beats fancier algorithms.
In other words… garbage in gets you garbage out. Even if you forget everything else from this course, please remember this point.
Remove Unwanted observations
The first step to data cleaning is removing unwanted observations from your dataset.
This includes duplicate or irrelevant observations.

Duplicate observations
Duplicate observations most frequently arise during data collection, such as when you:
- Combine datasets from multiple places
- Scrape data
- Receive data from clients/other departments
Fix Structural Errors
The next bucket under data cleaning involves fixing structural errors.
Structural errors are those that arise during measurement, data transfer, or other types of “poor housekeeping.”

As you can see:
- ‘composition’ is the same as ‘Composition’
- ‘asphalt’ should be ‘Asphalt’
- ‘shake-shingle’ should be ‘Shake Shingle’
- ‘asphalt,shake-shingle’ could probably just be ‘Shake Shingle’ as well
Filter Unwanted Outliers
Outliers can cause problems with certain types of models. For example, linear regression models are less robust to outliers than decision tree models.
In general, if you have a legitimate reason to remove an outlier, it will help your model’s performance.

Handle Missing Data
Missing data is a deceptively tricky issue in applied machine learning.
First, just to be clear, you cannot simply ignore missing values in your dataset. You must handle them in some way for the very practical reason that most algorithms do not accept missing values.
Unfortunately, from our experience, the 2 most commonly recommended ways of dealing with missing data actually suck.
They are:
- Dropping observations that have missing values
- Imputing the missing values based on other observations
Dropping missing values is sub-optimal because when you drop observations, you drop information.
- The fact that the value was missing may be informative in itself.
- Plus, in the real world, you often need to make predictions on new data even if some of the features are missing!
Imputing missing values is sub-optimal because the value was originally missing but you filled it in, which always leads to a loss in information, no matter how sophisticated your imputation method is.
- Again, “missingness” is almost always informative in itself, and you should tell your algorithm if a value was missing.
- Even if you build a model to impute your values, you’re not adding any real information. You’re just reinforcing the patterns already provided by other features.
Chapter 4: Feature Engineering
What is Feature Engineering?
Feature engineering is about creating new input features from your existing ones.
In general, you can think of data cleaning as a process of subtraction and feature engineering as a process of addition.
Infuse Domain Knowledge
You can often engineer informative features by tapping into your (or others’) expertise about the domain.
Try to think of specific information you might want to isolate. Here, you have a lot of “creative freedom.”

Create Interaction Features
The first of these heuristics is checking to see if you can create any interaction features that make sense. These are combinations of two or more features.
By the way, in some contexts, “interaction terms” must be products between two variables. In our context, interaction features can be products, sums, or differences between two features.

Combine Sparse Classes
The next heuristic we’ll consider is grouping sparse classes.
Sparse classes (in categorical features) are those that have very few total observations. They can be problematic for certain machine learning algorithms, causing models to be overfit.
Add Dummy Variables
Most machine learning algorithms cannot directly handle categorical features. Specifically, they cannot handle text values.
Therefore, we need to create dummy variables for our categorical features.
Dummy variables are a set of binary (0 or 1) variables that each represent a single class from a categorical feature.
Remove Unused Features
Finally, remove unused or redundant features from the dataset.
Unused features are those that don’t make sense to pass into our machine learning algorithms.

Chapter 5: Algorithm Selection
How to Pick ML Algorithms
In this lesson, we’ll introduce 5 very effective machine learning algorithms for regression tasks. They each have classification counterparts as well.
And yes, just 5 for now. Instead of giving you a long list of algorithms, our goal is to explain a few essential concepts (e.g. regularization, ensembling, automatic feature selection) that will teach you why some algorithms tend to perform better than others.
Why Linear Regression is Flawed
To introduce the reasoning for some of the advanced algorithms, let’s start by discussing basic linear regression. Linear regression models are very common, yet deeply flawed.

Regularization in Machine Learning
This is the first “advanced” tactic for improving model performance. It’s considered pretty “advanced” in many ML courses, but it’s really pretty easy to understand and implement.
The first flaw of linear models is that they are prone to be overfit with many input features.
Regularized Regression Algos
There are 3 common types of regularized linear regression algorithms.
![]()
Lasso, or LASSO, stands for Least Absolute Shrinkage and Selection Operator.
![]()
Ridge stands Really Intense Dangerous Grapefruit Eating (just kidding… it’s just ridge).
![]()
Elastic-Net is a compromise between Lasso and Ridge.
Decision Tree Algos
Awesome, we’ve just seen 3 algorithms that can protect linear regression from overfitting. But if you remember, linear regression suffers from two main flaws:
- It’s prone to overfit with many input features.
- It cannot easily express non-linear relationships.
Tree Ensembles
Ensembles are machine learning methods for combining predictions from multiple separate models. There are a few different methods for ensembling, but the two most common are:
Bagging
Bagging attempts to reduce the chance overfitting complex models.
- It trains a large number of “strong” learners in parallel.
- A strong learner is a model that’s relatively unconstrained.
- Bagging then combines all the strong learners together in order to “smooth out” their predictions.
Boosting
Boosting attempts to improve the predictive flexibility of simple models.
- It trains a large number of “weak” learners in sequence.
- A weak learner is a constrained model (i.e. you could limit the max depth of each decision tree).
- Each one in the sequence focuses on learning from the mistakes of the one before it.
- Boosting then combines all the weak learners into a single strong learner.
![]()
Random forests train a large number of “strong” decision trees and combine their predictions through bagging.
![]()
Boosted trees train a sequence of “weak”, constrained decision trees and combine their predictions through boosting.
Chapter 6: Model Training
How to Train ML Models
At last, it’s time to build our models!
It might seem like it took us a while to get here, but professional data scientists actually spend the bulk of their time on the steps leading up to this one:
- Exploring the data.
- Cleaning the data.
- Engineering new features.
Again, that’s because better data beats fancier algorithms.
Split Dataset
Let’s start with a crucial but sometimes overlooked step: Spending your data.
Think of your data as a limited resource.
- You can spend some of it to train your model (i.e. feed it to the algorithm). *You can spend some of it to evaluate (test) your model.
- But you can’t reuse the same data for both!

What are Hyperparameters?
So far, we’ve been casually talking about “tuning” models, but now it’s time to treat the topic more formally.
When we talk of tuning models, we specifically mean tuning hyperparameters.
There are two types of parameters in machine learning algorithms.
What is Cross-Validation?
Next, it’s time to introduce a concept that will help us tune our models: cross-validation.
Cross-validation is a method for getting a reliable estimate of model performance using only your training data.
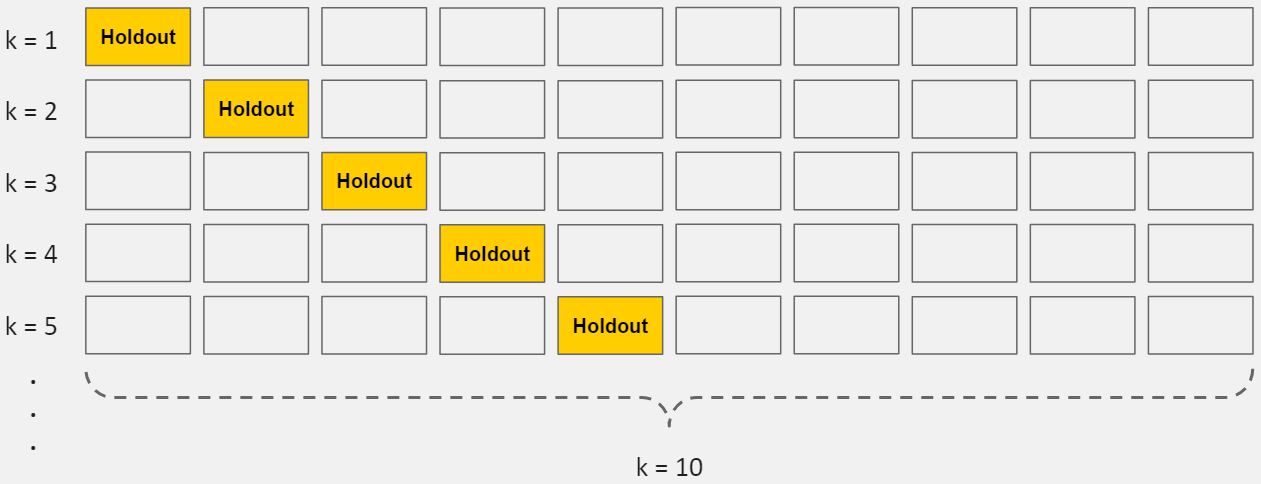
Fit and Tune Models
Now that we’ve split our dataset into training and test sets, and we’ve learned about hyperparameters and cross-validation, we’re ready fit and tune our models.
Basically, all we need to do is perform the entire cross-validation loop detailed above on each set of hyperparameter values we’d like to try.
Select Winning Model
By now, you’ll have 1 “best” model for each algorithm that has been tuned through cross-validation. Most importantly, you’ve only used the training data so far.